Случайная величина X принимает значения {3, 6, 7, 17}. Случайная величина Y принимает значения {7, 9, 12, 15}. Дан закон распределения двумерной случайной величины (X,Y) в виде матрицы (X - строки, Y - столбцы):
- Статистика
Условие:
Случайная величина X принимает значения {3, 6, 7, 17}. Случайная величина Y принимаетзначения {7, 9, 12, 15}. Дан закон распределения двумерной случайной
величины (X,Y) в виде матрицы (X - строки, Y - столбцы):
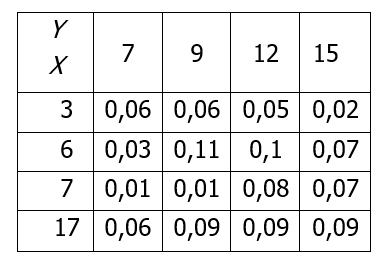
Найти: законы распределения составляющих X и Y (P(X),P(Y)), их математические ожидания (М(Х),М(Y)), дисперсии (D(X),D(Y)) и среднеквадратические отклонения (σ(X), σ(Y)); функцию регрессии Y на X (M(Y|x)); корреляционный момент (μ) и коэффициент корреляции (r).
Найти уравнение прямой средней квадратической регрессии Y на X. Построить её график с нанесёнными точками функции регрессии Y на X (M(Y|x)).
Решение:
Составим одномерные законы распределения случайных величин, требуя выполнения закона нормировки ipi = 1:
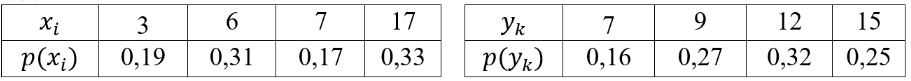
Математическое ожидание:
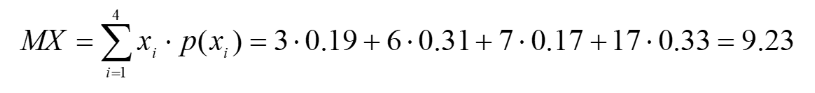
Дисперсия:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства