Требуется провести статистическую обработку заданной выборки, извлеченной из генеральной совокупности некоторой случайной величины X , закон распределения и числовые характеристики которой не известны.
- Статистика
Условие:
Требуется провести статистическую обработку заданной выборки, извлеченной из генеральной совокупности некоторой случайной величины X , закон распределения и числовые характеристики которой не известны.
Статистическую обработку следует провести в три этапа
На первом этапе нужно провести первичную обработку статистических данных, т.е.
1) составить группированный ряд распределения;
2) построить эмпирическую функцию распределения, ее график и кумуляту;
3) вычислить плотности относительных частот, построить гистограмму и полигон относительных частот;
4) получить точечные статистические оценки для математического ожидания, дисперсии, среднего квадратичного отклонения и медианы;
На втором этапе нужно проверить гипотезу о нормальном распределении генеральной совокупности X по критерию Пирсона. Для этого
1) выдвинуть основную и конкурирующую гипотезы о гипотетическом законе распределения;
2) вычислить теоретические частоты, используя функцию распределения гипотетического закона;
3) построить на одном рисунке полигон относительных частот и теоретическую кривую, сравнить эти кривые между собой;
4) выбрать статистический закон распределения (в данной работе критерий Пирсона) и вычислить наблюдаемое значение критерия;
5) задав уровень значимости и определив число степеней свободы, найти критическое значение критерия и принять основную или конкурирующую гипотезу.
Если генеральная совокупность распределена по нормальному закону, то на третьем этапе построить доверительные интервалы для математического ожидания и дисперсии. Если гипотеза о нормальном распределении на втором этапе отвергнута, то для построения доверительных интервалов для математического ожидания и дисперсии можно использовать те же формулы, что и для нормального распределения, если объем выборки достаточно велик (≥ 50). В этом случае доверительные интервалы будут найдены приближенно.
Исходные данные:
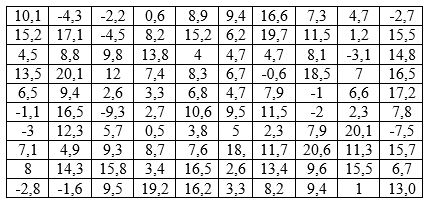
Решение:
I этап
1. Построение группированного статистического ряда
1) Наименьшее выборочное значение 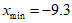 , наибольшее выборочное значение , объем выборки n = 100
, наибольшее выборочное значение , объем выборки n = 100
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства