В качестве исходных данных предлагаются наблюдения по пятидесяти районам урожайность гречихи и количество выпавших за год осадков. Для статистической обработки этих данных требуется: Для величин Х и Y составить группированные ряды.
- Статистика
Условие:
В качестве исходных данных предлагаются наблюдения по 50 районам урожайность гречихи (Y, ц/га) и количество выпавших за год осадков (X, см). Для статистической обработки этих данных требуется:
1) Для величин Х и Y составить группированные ряды.
2) На основании этих рядов построить полигоны и гистограммы частот.
3) Определить следующие показатели для Х и Y: точечные оценки (выборочные средние, исправленные выборочные дисперсии, исправленные квадратические отклонения), абсолютные и относительные ошибки выборочных средних.
4) Определить доверительные интервалы, в которых с надежностью γ=0,95 находятся среднее количество выпавших за год осадков и средняя урожайность гречихи.
5) Проверить гипотезу о нормальном распределении урожайности Y при уровне значимости α=0,05, используя критерий Пирсона.
6) Построить на одном чертеже эмпирическую и теоретическую кривые урожайности хозяйств;
7) Построить диаграмму рассеяния. Вычислить выборочный коэффициент корреляции.
8) Написать выборочные уравнения прямых линий регрессии Y на Х и Х на Y. Построить их в одной системе координат.
9) Сделать выводы для урожайности.
Таблица 1 – Исходные данные
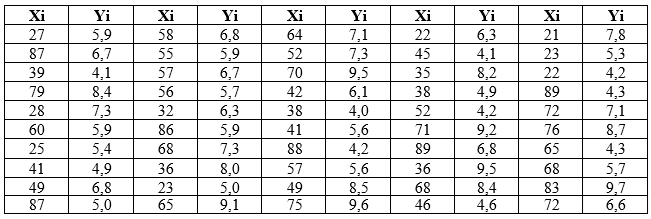
Решение:
1) Дана выборка значений случайной величины Х количества выпавших осадков с объемом n = 50. Очевидно, что она имеет непрерывное распределение, поэтому необходимо составить интервальное распределение Х. Обработку данных проведем в следующем порядке. Введем данные для Х. Построим вариационный ряд значений Х (используя средства MS Excel): с помощью процедуры Сортировка (по возрастанию) в меню Данные.
Для составления статистического распределения частот и относительных частот (табл. 2) выполним следующее (используя средства MS Excel). Вычислим размах варьирования: R =xmax xmin= 89-21 = 68 см. Опр...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства