Условие задачи
1. Возьмите 10 монет одинакового достоинства, хорошо перемешайте и выложите на стол. Сосчитайте количество гербов. Запишите результат.
2. Повторите пункт 1 сто раз. Результаты оформите в виде таблицы экспериментальных данных:
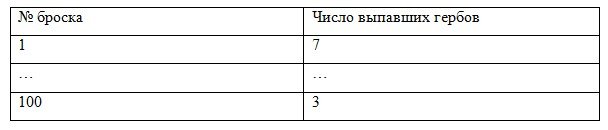
3. Сосчитайте, сколько раз выпало 0 гербов, 1 герб, 2 герба, 3 герба,…, результаты оформите в виде статистического ряда:
4. Постройте полигон частот, гистограмму.
5. Вычислите математическое ожидание a случайной величины X, ее дисперсию D и среднее квадратичное отклонение σ.
6. На графике, показывающем полигон относительных частот экспериментальных значений величины X, постройте кривую нормального распределения с вычисленными выше значениями математического ожидания и дисперсии.
7. Сравните экспериментальный и теоретический графики визуально.
8. Вычислите вероятности попадания случайной величины X в интервалы [a-σ;a+σ],[a-2σ;a+2σ],[a-3σ;a+3σ] и сравните с экспериментальными данными.
9. Вычислите критерий χ2 Пирсона и проверьте гипотезу о характере распределения (нормальное, биномиальное), приняв доверительную вероятность α=0,05.
10. Постройте доверительный интервал для математического ожидания величины X.
Ответ
1;2) После выполнения пунктов 1 и 2 получены результаты:
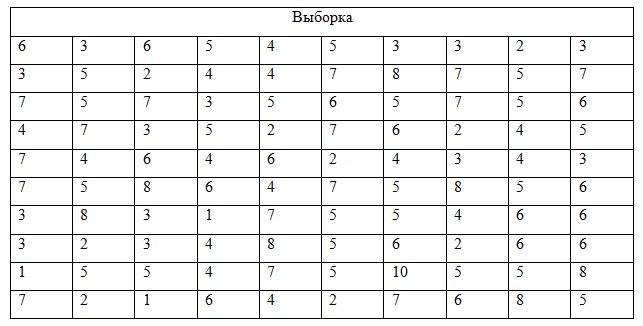
3) По выборке строим статистический ряд:
4) Построим полигон и гистограмму:
