Заменив неизвестные параметры генеральной совокупности соответственно их наилучшими выборочными оценками, по данным задачи 4, используя χ^2-критерий Пирсона на уровне значимости α=0.05, проверить две гипотезы о том, что изучаемая случайная

10 апреля 2025
Статистика

Условие:

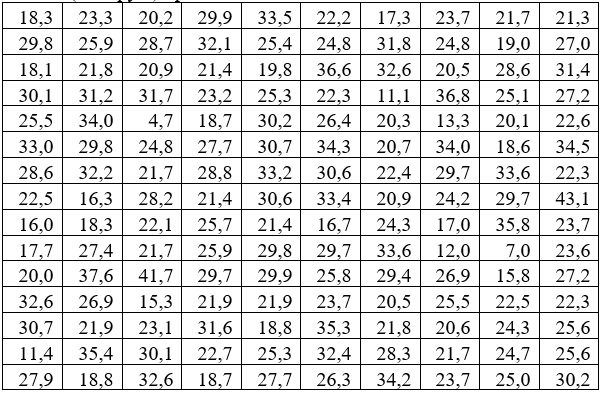
С целью определения средней величины месячной заработанной платы работников торговой сферы в некотором крупном районе города, по схеме собственно-случайной бесповторной выборки было отобрано 150 работников из 1300. Распределение месячной заработной платы (тыс. руб.) представлено в таблице:

Заменив неизвестные параметры генеральной совокупности соответственно их наилучшими выборочными оценками, используя -критерий Пирсона на уровне значимости , проверить две гипотезы о том, что изучаемая случайная величина - месячная заработная плата работников торговой сферы города - распределена:

а) по нормальному закону распределения;

б) по равномерному закону распределения.

Построить на чертеже, где изображена гистограмма эмпирического распределения, соответствующие графики равномерного и нормального распределений.

Исходные данные:

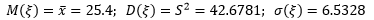
Решение:

Заменим неизвестные параметры генеральной совокупности их наилучшими выборочными оценками, то есть положим

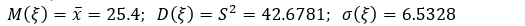
а) Проверим по критерию Пирсона гипотезу о том, что изучаемая случайная величина - величина недельного объема выполненных работ - распределена по нормальному закону с параметрами .