Условие задачи
Заменив неизвестные параметры генеральной совокупности соответственно их наилучшими выборочными оценками, по данным задачи 4, используя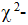 
критерий Пирсона, на уровне значимости 
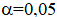проверить две гипотезы о том, что изучаемая случайная величина ξ – производительность труда на предприятий молочной промышленности – распределена:
а) по нормальному закону распределения;
б) по равномерному закону распределения.
Построить на чертеже, где изображена гистограмма эмпирического распределения, соответствующие графики равномерного и нормального распределений.
Ответ
Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона:
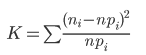
где pi вероятность попадания в i-й интервал случайной величины, распределенной по гипотетическому закону.
Для вычисления вероятностей pi применим формулу и таблицу функции Лапласа:
