Груз М массой m начинает движение из точки D с начальной скоростью V0. Его движение происходит по наклонной плоскости длины l, составляющей угол α с горизонтом вдоль линии АВ наибольшего ската.

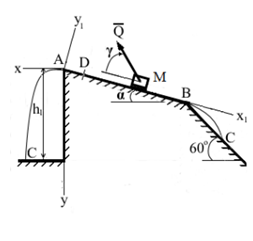
Груз М массой m начинает движение из точки D с начальной скоростью V₀. Его движение происходит по наклонной плоскости длины l, составляющей угол α с горизонтом вдоль линии АВ наибольшего ската. Положение точки D задается величиной AD = S₀, вектор начальной скорости V0 направлен параллельно прямой АВ к точке В. При движении по плоскости,  на груз действует постоянная сила Q, направление которой задается углом γ; коэффициент трения скольжения между грузом и наклонной плоскостью равен f. Через τ с груз покидает плоскость или в точке A, или в точке B и, двигаясь далее в вертикальной плоскости под действием только силы тяжести, через T секунд после отделения от плоскости попадает в точку С. Считая груз материальной точкой найти:

–точку (А или В) отрыва груза от плоскости;

–время τ движения груза по наклонной плоскости;

–скорость груза V_B (или V_A) в момент отрыва;

–координаты X_C, Y_C точки C приземления груза;

–время T движения груза в воздухе;

–скорость V_C груза в точке падения.