Условие задачи
Механическая система состоит из четырёх цилиндров, связанных между собой нерастяжимыми тросами. Каток 1 массы m1 =4m радиуса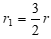 
катится без скольжения по неподвижной плоскости, наклонённой под углом α =300 к горизонту. Блоки 2 и 3 – одинаковые сплошные однородные сдвоенные цилиндры массы m2 = m3 =20m с внутренним радиусом 
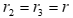и наружным радиусом 
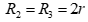. Даны радиусы инерции цилиндров: 
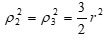. Система приводится в движение из состояния покоя моментом 
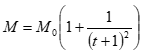, приложенным к катку 1.
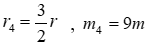
Необходимо:
1. Используя общие теоремы динамики, составить систему уравнений, описывающих движение заданной механической системы. Исключая из этой системы уравнений внутренние силы, получить дифференциальное уравнение, служащее для определения зависимости s(t) координаты точки A от времени – дифференциальное уравнение движения системы.
2. Получить то же самое дифференциальное уравнение движения системы, используя теорему об изменении кинетической энергии механической системы в дифференциальной форме.
3. Получить дифференциальное уравнение движения механической системы на основании общего уравнения динамики.
4. Убедившись в совпадении результатов, полученных тремя независимыми способами, проинтегрировать дифференциальное уравнение движения системы, получив зависимость s(t) координаты точки A от времени.
5. Определить натяжения тросов в начальный момент времени (при t= 0).
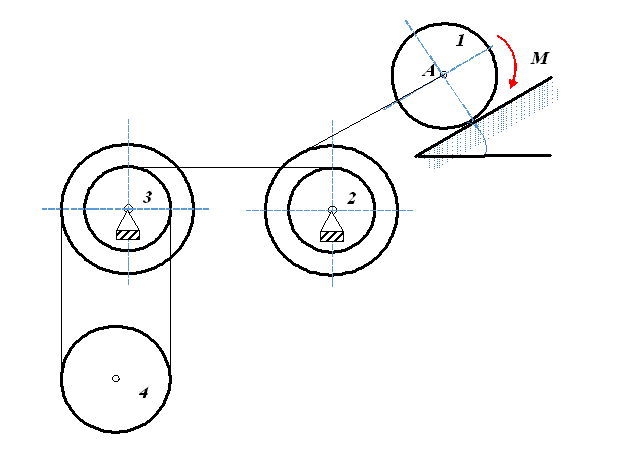
Рис 1
Ответ
Колесо 1 совершает плоскопараллельное движение. Одну из осей координат направим вниз по наклонной плоскости (в сторону движения центра колеса). Дифференциальные уравнения движения имеют вид:
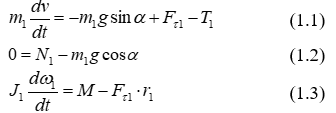
Колеса 2 и 3 совершают вращательное движение. Дифференциальные уравнения движения имеют вид:
