Условие задачи
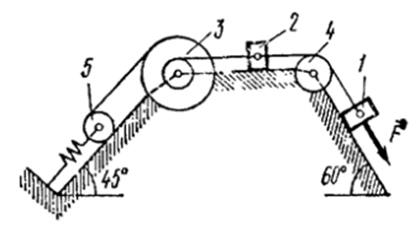
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней 𝑅3 = 0,3 м, 𝑟3 = 0,1 м и радиусом инерции относительно оси вращения 𝜌3 = 0,2 м, блока 4 радиуса 𝑅4 = 0,2 м и катка (или подвижного блока) 5; тело 5 считать сплошным однородным цилиндром, а массу блока 4 – равномерно распределенной по ободу. Коэффициент трения груза о плоскость 𝑓 = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости c. Под действием силы 𝐹 = 𝑓(𝑠), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в начальный момент времени равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным 𝑠1 = 0,2 м. Искомая величина « ω4».
Все катки, включая и катки обмотанные нитями, катятся по плоскостям без скольжения.
Ответ
1. Рассмотрим движение неизменяемой механической системы, состоящей из весомых тел 2, 4, 5 и невесомых 1 и 3 (тело 1 - удаляем, не показываем на рисунке). Изображаем, действующие на систему внешние силы:
а) активные F, Fупр, Р2, Р3, Р4, Р5, сила Р3 = 0 и изображена формально;
б) реакции N2, N3, N4, N5, реакция N3 = 0 и изображена формально;
в) сила трения F2тр
г) момент от сил сопротивления М.
Для определения величины 4 воспользуемся теоремой об изменение кинетической энергии механической системы:
