Механизм состоит из двух вращающихся на неподвижных осях блоков, соединенных нерастяжимым ремнем. Блоки передают движение грузам. Задан закон изменения скорости одного из грузов (в см/с). В указанный момент времени найти скорость другого груза и ускорение точки М на внутреннем ободе блока А.
RА = 40 cм; rА = 30cм; RВ = 25см; rB = 10 cм; Vc = 36t2 cм/c, t1 =1,2 c.
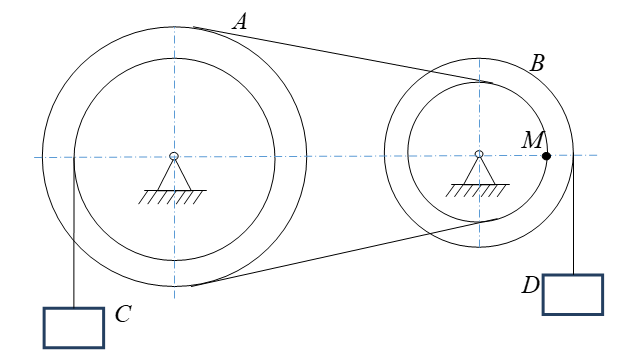
Рисунок 1.
Найдем ускорение груза C:
ac = dvc / dt = d(36t2) / dt = 72t см/с2
При t1 = 1,2 с:
vD = 36 1,22 = 51,84 см/с значение скорости положительно, направим вектор скорости вертикально вверх.
ас = 72 1,2=86,4 см/с2 значение ускорения положительно, направим вектор ускорения вертикально вверх (рис.2).
Так как блок A и груз C соединены нерастяжимой нитью, то линейные скорости точки схода нити блока A и груза C равны между собой. Тогда по формуле для скорости точки вращающегося вокруг неподвижной оси тела можно записать:
vC = A rА ⟹ A = vC / rА
Продифференцировав обе части уравнения, получим, ч...