Условие задачи
Каток 1 массой m1, на который намотан нерастяжимый канат, катится без скольжения по горизонтальной плоскости из состояния покоя под действием момента М пары сил и поднимает канатом, перекинутым через блок 2 массой m2 , груз 3 массой m3, по наклонной плоскости, образующей угол α с горизонтом (рис.1). Пренебрегая трением качения катка с плоскостью и проскальзыванием нити относительно блока и катка, найти ускорение движения центра масс груза. Принять, что каток и блок представляют собой сплошные однородные цилиндры радиусами R1 и R2, участок каната между блоком и катком горизонтальный и коэффициент трения скольжения при движении груза по плоскости равен μ.
М=23Н∙м; m1=32кг; R1=0,16м; m2=8кг; R2=0,56м; m3=13кг; α=450; μ=0,1
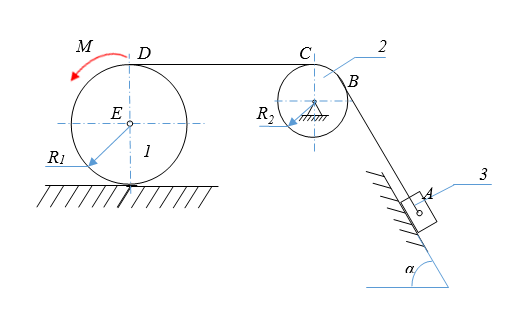
Рис.1
Ответ
Тела 1,2,3, соединенные канатом, образуют механическую систему. Движения тел плоскопараллельные. Оси вращения катка и колеса перпендикулярны плоскости, в которой происходит движение.
Обозначим как 
угловые скорости вращения блока и колеса, vA, vB, vC, vD, vE - скорости точек А,В,С,D касания каната с грузом, блоком, колесом и центра Е масс колеса.
Будем считать, что угол поворота тела вокруг оси ...
