Решение задачи
Точка эм движется по диску (по ободу). Диск вращается вокруг оси, проходящей через точку о один и перпендикулярной плоскости диска, в направлении, указанном стрелкой, с постоянной угловой скоростью.
- Теоретическая механика
Условие:
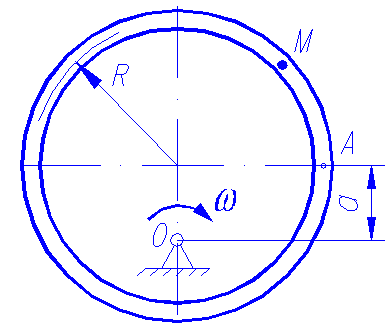
Точка М движется по диску (по ободу) согласно закону S = AM = f(t). Диск вращается вокруг оси, проходящей через точку О1 и перпендикулярной плоскости диска, в направлении, указанном стрелкой, с угловой скоростью ω = const. Определить абсолютную скорость точки М в момент времени t1.
S = 2(t2 - t), см; t1 = 2 с; ω = 0,1с-1; R = 80 см; а = 30 см.
Решение:
Дано:
S = 2(t2 - t), см;
t1 = 2 с;
= 0,1с-1;
R = 80 см;
а = 30 см.
Точка М совершает сложное движение: относительное вращательное по ободу диска, и переносное вращательное вместе с диском вокруг точки О.
В момент времени t1 = 2c пройденный путь относительного движения:
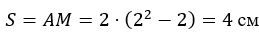
точка движется в сторону заданного положительного направления.
При этом центральный угол составит:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
Р
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э