Условие задачи
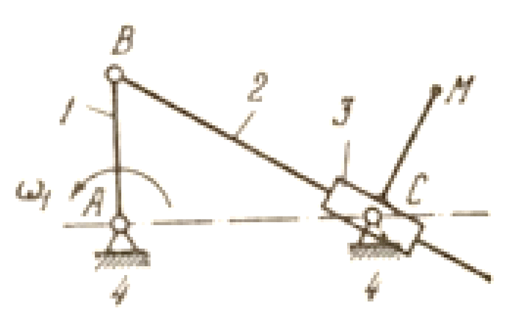
Для кривошипного механизма с качающимся ползуном определить скорость точки М, лежащей на плоскости, которая связана с ползуном 3.
Дано:
ω1=20 с1, lAB = 100 мм, lAС = 173 мм, МС перпендикулярно ВС, lСМ = 100 мм,
∠ВАС = 90°
Ответ
Треугольник АВС, согласно условия - прямоугольный ( ВАС = 90). Определяем величину гипотенузы ВС и угла АСВ = :
lBC = [(lAB)2 +(lAC)2]1/2 = (1002 + 1732)1/2 = 200 мм.
sin = lAB/ lBC = 100/200 = 0,5; следовательно = 30.
На основании теоремы о сложении скоростей скорость точки С, принадлежащей звену 2 (ВС), можно определить, решим систему векторных уравнений:
, т.к. точка С3 (точка С, принадлежащая звену 3) - неподвижна (принадлежит стойке), ⟘ ВС, а ‖ ВС, а модуль скорости
Потяни
