1. Главная
  2. Библиотека
  3. Теория вероятностей
  4. 1. В студенческой группе 5 отличников, 4 хороших студента и 3 троечника. Отличник всегда сдает экзамен на 5, хороший студе...

1. В студенческой группе 5 отличников, 4 хороших студента и 3 троечника. Отличник всегда сдает экзамен на 5, хороший студент – на 4 и троечник – на 3. Случайным образом были выбраны два студента и проэкзаменованы.

«1. В студенческой группе 5 отличников, 4 хороших студента и 3 троечника. Отличник всегда сдает экзамен на 5, хороший студент – на 4 и троечник – на 3. Случайным образом были выбраны два студента и проэкзаменованы.»
  • Теория вероятностей

Условие:

1. В студенческой группе 5 отличников, 4 хороших студента и 3 троечника. Отличник всегда сдает экзамен на 5, хороший студент – на 4 и троечник – на 3. Случайным образом были выбраны два студента и проэкзаменованы. Средний балл по этому экзамену – случайная величина. Написать ее закон распределения. 

2. Дискретная случайная величина X задана законом распределения: 

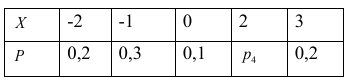
Найти вероятность p4, функцию F(x), ее график, M(X) и D(X). 

 

Решение:

1.Если экзаменовались два отличника, то средний балл 5. Два отличника попадают в выборку с вероятностью С25 / С212 = 5/33. Если экзаменовались отличник и хороший студент, то средний балл равен 4,5. Такой состав выборки получается с вероятностью 5*4/ С212 = 10 / 33. Средний балл равен 4, если в выборку попали два хороших студента. Такой же средний балл получается, если в выборке отличник и троечник. Суммарная вероятность этих событий С24 / С212 + 5*3 / С212 = 7 / 22. Средний балл равен 3,5, еслиэкзаменовали хорошего студента и троечника. Вероятность такого состававыборки равна 4*3 / С212 = 2 /...

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я