1. Главная
  2. Библиотека
  3. Теория вероятностей
  4. Дано статистическое распределение выборки (в первой строке указаны выборочные варианты ξi, а во второй строке – соответств...

Дано статистическое распределение выборки (в первой строке указаны выборочные варианты ξi, а во второй строке – соответственные частоты ni количественного признака ξ). Найдите: 1) методом произведений – выборочное среднеквадратичное отклонение,

«Дано статистическое распределение выборки (в первой строке указаны выборочные варианты ξi, а во второй строке – соответственные частоты ni количественного признака ξ). Найдите: 1) методом произведений – выборочное среднеквадратичное отклонение,»
  • Теория вероятностей

Условие:

Дано статистическое распределение выборки (в первой строке указаны выборочные варианты ξi, а во второй строке – соответственные частоты ni количественного признака ξ).

Найдите:

1) методом произведений 

– выборочное среднеквадратичное отклонение, 

– выборочную дисперсию;

2) доверительные интервалы для оценки неизвестного математического ожидания  с заданной надежностью γ = 0,95.

Пользуясь критерием Пирсона, при уровне значимости 0,05 установить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с данными выборки объема n = 100. 

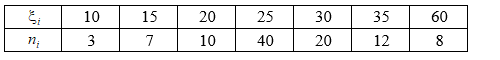
Решение:

1) Составим расчетную таблицу.

В качестве ложного нуля выберем варианту 25.

Условные варианты найдем из выражения

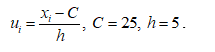
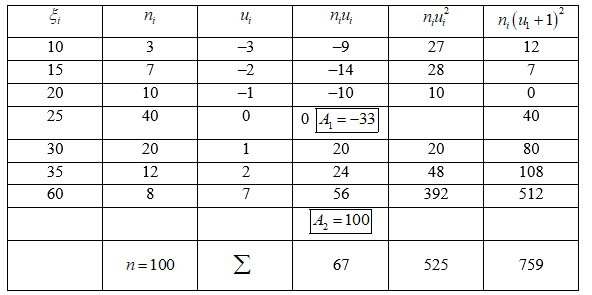
Контроль:

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я