Условие задачи
Дискретные случайные величины X1 и X2 имеют биномиальное и пуассоновское распределение соответственно. Известны математические ожидания каждой из величин: M(X1 )=M(X2 )=6, и дисперсия величины X1:D(X1 )=3/2. Для каждой из величин най¬дите вероятность, что она попадет в отрезок [3; 5].
Ответ
1) Для биномиального распределения математическое ожидание определяется по формуле:
M(x)=np,
где n - число испытаний, p вероятность появления события в каждом испытании.
Дисперсия для биномиального распределения может быть определена по формуле:
D(x)=npq,
где q = 1 p.
Учитывая условия задачи, имеем
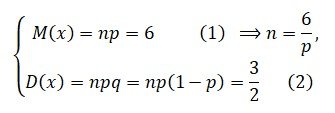
тогда подставив в (2) имеем
Потяни
