1. Главная
  2. Библиотека
  3. Теория вероятностей
  4. Для непрерывной случайной величины (н. с. в.) X задана функция распределения F(x) (плотность функции распределения f(x))....

Для непрерывной случайной величины (н. с. в.) X задана функция распределения F(x) (плотность функции распределения f(x)). Вычислить соответствующую плотность функции распределения f(x) (функцию распределения F(x)).

«Для непрерывной случайной величины (н. с. в.) X задана функция распределения F(x) (плотность функции распределения f(x)). Вычислить соответствующую плотность функции распределения f(x) (функцию распределения F(x)).»
  • Теория вероятностей

Условие:

Для непрерывной случайной величины (н. с. в.) X задана функция распределения F(x) (плотность функции распределения f(x)). Вычислить соответствующую плотность функции распределения f(x) (функцию распределения F(x)). Проверить выполнение условия нормировки распределений. Построить графики обеих функций. Вычислить числовые характеристики распределений: математическое ожидание M(X) и дисперсию D(X). Вычислить вероятность того, что н. с. в. X примет значения из заданного интервала (a; b) = (¼; ¾). Примечание: C1, C2 = const.

Н. с. в. задана функцией распределения

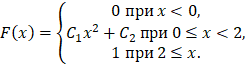
Решение:

Функция распределения должна быть непрерывна в любой точке. Пользуясь этим, определим неизвестные константы 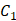и . Так как в точках функция распределения также должна быть непрерывна, получаем систему уравнений для нахождения неизвестных и

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я