Условие задачи
Для заданной выборки из генеральной совокупности случайной величины Х (n=100) необходимо:
а) определить размах варьирования случайной величины и составить вариационный ряд распределения;
б) по формуле Стерджеса определить длину интервалов и составить интервальный вариационный ряд;
в) найти выборочную среднюю хв, выборочную дисперсию Dв, выборочное среднее квадратическое отклонение σв, моду Мо, медиану Ме; коэффициент вариации δв;
г) построить эмпирическую функцию распределения вероятностей F*(x);
д) построить гистограмму относительных частот и линию эмпирической плотности.
Ответ
а) определим размах варьирования случайной величины и составим вариационный ряд распределения.
Минимальное значение min xi = 47 , максимальное max xi = 69.
Размах вариации:
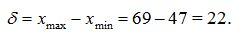
Так как вариация значительна, то дискретный ряд составлять не целесообразно.
Упорядочим данные по возрастанию:
