Условие задачи
1. Два датчика посылают сигнал в общий канал связи, причем первый из них посылает вдвое больше сигналов, чем второй. Вероятность получить искаженный сигнал от первого датчика равна 0,06, от второго – 0,03. Какова вероятность получить искаженный сигнал в общем канале
2. В вычислительной лаборатории имеется 6 клавишных автоматов и 4 полуавтомата. Вероятность того, что за время выполнения некоторых расчетов автомат не выйдет из строя, равна 0,95; для полуавтомата эта вероятность равна 0,8. Студент производит расчет на наудачу взятой машине. Найти вероятность того, что до окончания расчетов машина не выйдет из строя.
3. В специализированную больницу поступают в среднем 50% больных с заболеванием К, 30% - с заболеванием Л, 20% - с заболеванием М. Вероятность полного излечения болезни К равна 0,7, для болезни Л – 0,8, для М – 0,9. Больной, поступивший в больницу, был выписан здоровым. Найти вероятность того, что этот больной страдал заболеванием К.
4. В спартакиаде участвуют из первой группы четыре студента, из второй - шесть и из третьей – пять. Студент первой группы попадает в сборную института с вероятностью 0,9, студент второй группы – 0,7, а студент третьей группы – 0,8. Наудачу выбранный студент попал в сборную института. Вероятнее всего, из какой он группы?
Ответ
1.Пусть событие A будет получен искаженный сигнал в общем канале связи.
Введём гипотезы:
H1-сигнал поступил от первого датчика;
H2-сигнал поступил от второго датчика.
Исходя из условия нам известны следующие вероятности:
P (H1) = 2/3
P (H1) = 1/3
P (A|H1) = 0,06
P (A|H2) = 0,03
Тогда по формуле полной вероятности искомая вероятность равна:
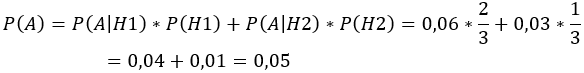
Ответ: 0,05
2.
Пусть событие A до окончания расчетов ...
