Два стрелка соревнуются по очереди стреляя в мишень по первого попадания. Вычислить значение, при котором шансы на победу у стрелков А и В равны
«Два стрелка соревнуются по очереди стреляя в мишень по первого попадания. Вычислить значение, при котором шансы на победу у стрелков А и В равны»
- Теория вероятностей
Условие:
Два стрелка соревнуются по очереди стреляя в мишень по первого попадания. Вероятность попадания в мишень стрелка А равна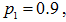 
, стрелка В 
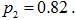. Право первого выстрела определяется жребием, в котором стрелок А побеждает вероятностью 
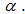Вычислить значение 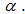, при котором шансы на победу у стрелков А и В равны
Решение:
Пусть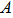 
- событие первый стрелок попал, В - событие второй стрелок попал и пусть - до окончания игры первый игрок вытащил шаров, тогда, если событие - первый игрок попадет при своем - ом выстреле. Если первый игрок выиграет при - ом выстреле - это означает, что первый и второй игрок промазали по разу, то есть
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э