Условие задачи
1. Из 200 задач первого раздела курса математики, предложенных для решения, абитуриенты решили 130, а из 300 задач второго раздела абитуриенты решили 120. Можно ли при a=0,01 утверждать, что первый раздел школьного курса абитуриенты освоили лучше, чем второй.
2.Проверка правильности функционирования устройства осуществляется специальным тестом. Если устройство функционирует правильно, то вероятность прохождения теста равна 0,99; в противном случае вероятность прохождения теста равна 0,4. Устройство допускается к работе, если тест проходит пять раз при пяти испытаниях. В предположении, что число прохождений теста в пяти испытаниях подчиняется биномиальному распределению, указать критическую область для проверки гипотезы о том, что устройство функционирует правильно, и вычислить вероятность ошибок первого и второго рода.
3. Два штурмана определяли пеленг маяка по нескольким замерам, используя различные пеленгаторы. Первый штурман произвел 4 замера, при этом выборочное среднее полученных результатов оказалось равным 70,2. Второй штурман произвел 9 замеров, выборочное среднее оказалось равным 70,5. В предположении, что результаты измерений имеют нормальное распределение со стандартным отклонением 0,5, проверить гипотезу о том, что различие результатов вызвано только случайными ошибками. Принять уровень значимости, равным 0,05.
Ответ
1.Пусть p1 процент абитуриентов, решающих задачи первого раздела;
p2 процент абитуриентов, решающих задачи второго раздела.
Введём нулевую гипотезу:
H0:p1 = p2
Конкурирующая гипотеза при этом выглядит так:
H0: p1 p2
Вычислим наблюдаемое значение критерия:
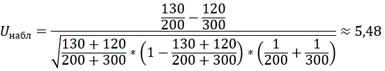
Найдём критическую точку:
