1. Главная
  2. Библиотека
  3. Теория вероятностей
  4. Какой процент деталей будет отклоняться от a не более чем на ±5 мм? Написать выражение для плотности распределения вероятн...

Какой процент деталей будет отклоняться от a не более чем на ±5 мм? Написать выражение для плотности распределения вероятностей и функции распределения этой случайной величины.

«Какой процент деталей будет отклоняться от a не более чем на ±5 мм? Написать выражение для плотности распределения вероятностей и функции распределения этой случайной величины.»
  • Теория вероятностей

Условие:

На станке изготовляются детали, длина которых должна равняться a см. Известно, что 75% деталей отклоняются от нормы не более чем на ±3 мм.

1) Какой процент деталей будет отклоняться от a не более чем на ±5 мм?

2) Написать выражение для плотности распределения вероятностей и функции распределения этой случайной величины;

3) Найти P (a < x < b); a = (a – 0,26)см; b =(a+0,52)см. Результат округлить до 0,001 и геометрически интерпретировать, используя построенные кривые.

Решение:

Вероятность того, что абсолютная величина |X-a| отклонения окажется меньше .

Вероятность того, что отклонение нормально распределенной случайной величины от ее математического ожидания по абсолютной величине не превзойдет некоторого положительного числа , то есть |X- a| , определяется так:

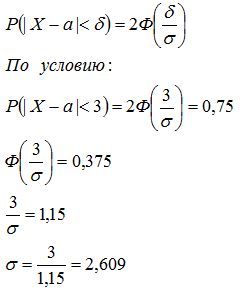
1) Найдем какой процент деталей б...

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я