1. Главная
  2. Библиотека
  3. Теория вероятностей
  4. Вероятность «сбоя» в работе телефонной станции при каждом вызове равна ноль, ноль ноль два. Поступило тысяча вызовов. Опре...

Вероятность «сбоя» в работе телефонной станции при каждом вызове равна ноль, ноль ноль два. Поступило тысяча вызовов. Определить вероятность одиннадцать «сбоев», при условии, что результат для каждого вызова не зависит от результатов по другим.

«Вероятность «сбоя» в работе телефонной станции при каждом вызове равна ноль, ноль ноль два. Поступило тысяча вызовов. Определить вероятность одиннадцать «сбоев», при условии, что результат для каждого вызова не зависит от результатов по другим.»
  • Теория вероятностей

Условие:

1. Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0,002. Поступило 1000 вызовов. Определить вероятность  11 «сбоев», при условии, что результат для каждого вызова не зависит  от результатов  по другим.

2. Вероятность наступления некоторого события в каждом из 200 независимых испытаний равна 0,8. Определить вероятность того, что число наступлений события m удовлетворяет следующему неравенству: .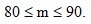

Решение:

1. Испытание состоит в проверке вызова. Число испытаний n=1000

Пусть событие A вызов завершился с сбоем

p=P(A)=0,002

Так как число испытаний достаточно велико, а =np=210, то вероятность того, что в n независимых повторных испытаниях событие A наступит ровно k раз, найдем с помощью формулы Пуассона:

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я