Найти величину коэффициента a , написать аналитическое выражение и простроить график функции распределения, найти математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины.
«Найти величину коэффициента a , написать аналитическое выражение и простроить график функции распределения, найти математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины.»
- Теория вероятностей
Условие:
Плотность распределения вероятностей непрерывной случайной величины задана выражением:
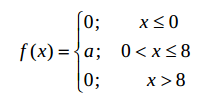
Найти величину коэффициента a, написать аналитическое выражение и простроить график функции распределения, найти математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины. Найти вероятности попадания данной случайной величины в интервалы (4, 6) и (6, 10).
Решение:
1) Здесь имеем дело с непрерывной с. в., имеющей ненулевую плотность вероятности только на интервале (0; 8), поэтому бесконечные пределы интегрирования в соответствующих формулах заменяем на конечные: от 0 до 8. Для нахождения постоянной a воспользуемся свойством плотности вероятности:
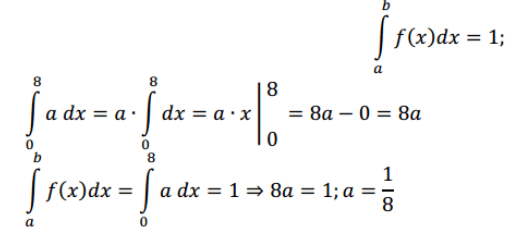
Таким образом,
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э