Найти вероятность того, что на втором и третьем шаге достанут чёрные шары, если в начальный момент времени в урне было равное число белых и черных шаров. Чему равна в вероятность вынуть черный шар два раза подряд в стационарном режиме?

23 января 2025
Теория вероятностей

Условие:

В урне находится 4 шара черного и белого цвета. На каждом шаге из урны берут 1 шар. Если выбранный шар – черный, то его с равными вероятностями заменяют на белый или черный шар, а если выбранный шар белый, то его заменяют на белый шар 2 раза чаще, чем на черный. Найти вероятность того, что на втором и третьем шаге достанут чёрные шары, если в начальный момент времени в урне было равное число белых и черных шаров. Чему равна в вероятность вынуть черный шар два раза подряд в стационарном режиме?

Решение:

Введем в рассмотрение цепь Маркова с состояниями S₀-S₄ , где индекс в обозначении соответствует числу черных шаров в урне, и определим вероятности переходов между состояниями. Отметим также, что черный шар заменяют на белый с вероятностью 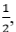, а белый на черный с вероятностью .