Написать закон распределения числа деталей сорта i среди отобранных. Построить функцию распределения и начертить ее график.
«Написать закон распределения числа деталей сорта i среди отобранных. Построить функцию распределения и начертить ее график.»
- Теория вероятностей
Условие:
Из ящика, содержащего N1 деталей первого сорта, N2 деталей второго сорта и N3 деталей третьего сорта, наудачу достали K изделий.
1. Написать закон распределения числа деталей сорта i среди отобранных.
2. Построить функцию распределения и начертить ее график.
3. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение полученной случайной величины.
4. Вычислить вероятность попадания случайной величины в промежуток (α,β).
Решение:
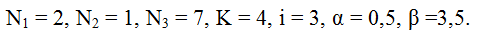
1. Всего в ящике 10 деталей: 2 детали 1-го сорта, 1 деталь 2-го сорта, 7 деталей 3-го сорта.
Х число деталей 3-го сорта среди 4-х отобранных.
Поскольку деталей 1-го и 2-го сорта всего 3, а отбирается 4 детали, в число отобранных обязательно попадет хотя бы одна деталь 3-го сорта.
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э