Условие:
Непрерывная случайная величина задана функцией распределения вероятностей F(x). Требуется:
а) найти плотность распределения вероятностей f(x)
б) найти математическое ожидание, дисперсию, средне квадратическое отклонение
в) вычислить вероятность попадания случайной величины в интервал (1;4)
г) построить графики функции распределения F(x) и плотности распределения f(x)
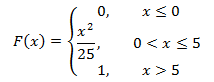
Решение:
Функцию плотности распределения вероятностей найдем как производную от функции распределения:
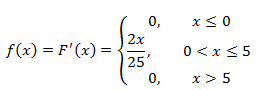
Математическое ожидание найдем по формуле:
