Условие задачи
Определить вероятность того, что корни а) квадратного x2+2ax+b=0, б) кубического x3+3ax+2b=0 уравнений вещественны, если равновозможны значения коэффициентов в прямоугольнике |a|≤n, |b|≤m. Какова вероятность того, что при указанных условиях корни квадратного уравнения будут положительны?
Ответ
а) Чтобы корни квадратного уравнения x2+2ax+b=0 были вещественными, необходимо выполнение условия D=(2a)2-4b04(a2-b)0ba^2;ba^2n^2.
Вероятность найдем по формуле геометрического определения вероятности. Возможны два случая:
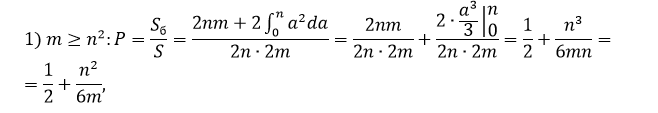
где S-геометрическая мера всей области (прямоугольник состоронами 2n и 2m-BEFG),Sб- геометрическая мера части этой области, попадание в которую благоприятствует тому, что корни...
Потяни
