1. Главная
  2. Библиотека
  3. Теория вероятностей
  4. Плотность вероятности f(x) случайной величины X имеет вид ломаной с вершинами (-2,0), (8,0) и (0,m). Требуется найти число...

Плотность вероятности f(x) случайной величины X имеет вид ломаной с вершинами (-2,0), (8,0) и (0,m). Требуется найти число m, математическое ожидание MX, дисперсию DX, функцию распределения F(x) и построить графики функций f(x) и F(x).

«Плотность вероятности f(x) случайной величины X имеет вид ломаной с вершинами (-2,0), (8,0) и (0,m). Требуется найти число m, математическое ожидание MX, дисперсию DX, функцию распределения F(x) и построить графики функций f(x) и F(x).»
  • Теория вероятностей

Условие:

Плотность вероятности f(x) случайной величины X имеет вид ломаной с вершинами (-2,0), (8,0) и (0,m). Требуется найти число m, математическое ожидание MX, дисперсию DX, функцию распределения F(x) и построить графики функций f(x) и F(x).

Решение:

Построим пояснительный рисунок и обозначим точки A(-2,0), C(8,0) и B(0,m)

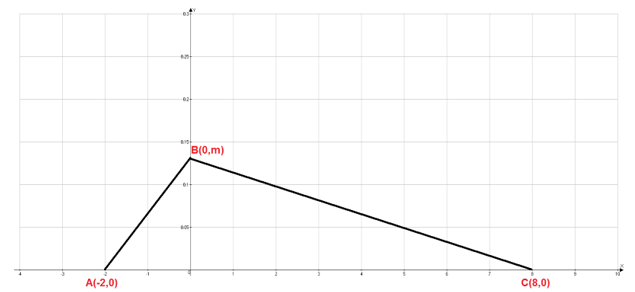
Из свойства нормировку функции плотности распределения вероятностей делаем вывод, что площадь треугольника ABC должна быть равна 1. Находим параметр m:

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я