Условие:
Плотность вероятности случайной величины 
имеет вид:
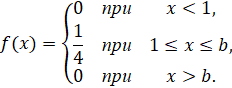
Найти:
а) параметр b;
б) математическое ожидание и дисперсию случайной величины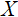 
;
в) функцию распределения F(x) и построить ее график.
Оценить с помощью неравенства Чебышева вероятность того, что случайная величина принимает значения на промежутке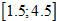 
. Вычислить эту вероятность с помощью функции распределения. Объяснить различие результатов.
Решение:
Параметр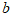 
определим из соотношения 
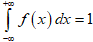, тогда получаем