Условие:
Предел прочности титанового сплава представляет собой нормально распределенную случайную величину с математическим ожиданием 1100 МПа и средним квадратическим отклонением 20 МПа.
Найти дифференциальную и интегральную функции распределения, построить их графики. Определить числовые характеристики. Найти вероятность того, что предел прочности случайно отобранной детали из титанового сплава будет менее 1050 МПА. Проиллюстрировать решение задачи графически.
Решение:
Математическое ожидание размера детали равно 200 мм., среднее квадратическое отклонение равно 2.5 мм.
М(Х)=1100 МПа = а
(Х)=20 МПа
D(X)= 2(Х)=400
Непрерывная случайная величина X, распределённая по нормальному закону, имеет функцию плотности:
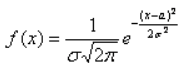
ифункцию распределения вероятностей: