Условие задачи
1. Произведено 300 испытаний, в каждом из которых неизвестная вероятность p появления события A постоянна. Событие A появилось в 250 испытаниях. Найти доверительный интервал, покрывающий неизвестную вероятность p с надежностью 0,95.
2. Найти доверительный интервал для оценки с надежностью 0,99 неизвестного математического ожидания a нормально распределенного признака X генеральной совокупности, если известны генеральное среднее, квадратическое отклонение, выборочная средняя и объём выборки: а) σ=4, x ̅ В=10,2, n=16 ; б) σ=5, x ̅ B=16, 8,n=25.
3. Из генеральной совокупности извлечена выборка объёма n=50. Найти несмещенную оценку генеральной средней.
Ответ
1. Найдём относительную частоту появления события A:
Найдём значение аргумента t:
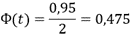
t = 1,96
Искомый доверительный интервал выглядит так:
p1pp2
Найдём неиз...
