Условие задачи
1. Рабочий изготовляет за смену 625 деталей. Вероятность того, что деталь окажется первого сорта, равна 0,8. Какова вероятность того, что деталей первого сорта будет ровно 510 штук?
2. Вероятность появления события A в каждом из 625 независимых испытаний равна 0,64. Найти вероятность того, что в этих испытаниях событие A появится от 400 до 430 раз.
Ответ
1. Так как в данном случае количество деталей достаточно велико, для нахождения искомой вероятности используем локальную теорему Лапласа:
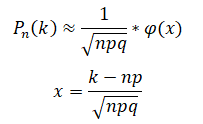
Исходя из условия, имеем, что:
Потяни
