Рассматривается простейшая n-канальная система массового обслуживания с m местами в очереди. Поступающий поток имеет интенсивность заявок в час. Среднее время обслуживания равно t минут. Найти предельное стационарное
«Рассматривается простейшая n-канальная система массового обслуживания с m местами в очереди. Поступающий поток имеет интенсивность заявок в час. Среднее время обслуживания равно t минут. Найти предельное стационарное»
- Теория вероятностей
Условие:
Рассматривается простейшая n-канальная система массового обслуживания с m местами в очереди. Поступающий поток имеет интенсивность заявок в час. Среднее время обслуживания равно t минут. Найти предельное стационарное распределение и характеристики эффективности этой СМО. n =3; m = 2;
Решение:
Вычисляем показатели обслуживания многоканальной СМО:
Интенсивность потока обслуживания:
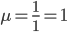
1. Интенсивность нагрузки.
= *tобс = 10*1 = 10
Интенсивность нагрузки =10 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания.
3. Вероятность, что канал свободен (доля времени простоя каналов).
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э