Условие:
С целью определения средней суммы вкладов на 1 января текущего года в сберегательном банке, имеющем 2000 вкладчиков, по схеме собственно-случайной выборки с бесповторным отбором членов проведено обследование 200 лицевых счетов. Распределение вкладов по их величине (тыс. руб.) представлено в таблице:
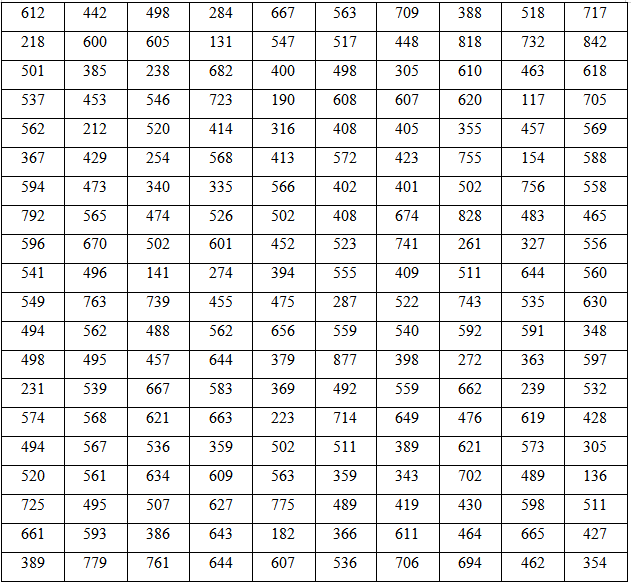
Составить интервальный вариационный ряд. Записать эмпирическую функцию распределения и построить ее график. На одном чертеже изобразить гистограмму и полигон частот.
По сгруппированным данным вычислить выборочные числовые характеристики: среднее арифметическое, исправленную выборочную дисперсию, среднее квадратичное отклонение, коэффициент вариации, асимметрию, эксцесс, моду и медиану.
Найти:
а) вероятность того, что средняя величина вклада в банке отличается от полученной по выборке не более чем на 500 руб.;
б) границы, в которых с вероятностью 0,95 заключена доля всех вкладов, сумма которых составляет не менее 500 тыс. руб.;
в) объем бесповторной выборки, при котором границы для генеральной средней величины вклада из п. а) можно гарантировать с вероятностью 0,97.
Решение:
Образуем 8 групп с равными интервалами.
Определим величину интервала группировки:
![]()
Тогда интервальный ряд распределения имеет вид: