Система состоит из (k+1) параллельно соединенных равнонадёжных подсистем, вероятность безотказной работы каждой из которых P(t)=ехр(–λt). Интенсивность отказов =0,2∙10^-4 1/час. Резерв пассивный с неизменной нагрузкой.
«Система состоит из (k+1) параллельно соединенных равнонадёжных подсистем, вероятность безотказной работы каждой из которых P(t)=ехр(–λt). Интенсивность отказов =0,2∙10^-4 1/час. Резерв пассивный с неизменной нагрузкой.»
- Теория вероятностей
Условие:
Система состоит из (k+1) параллельно соединенных равнонадёжных подсистем, вероятность безотказной работы каждой из которых P(t)=ехр(–λt). Интенсивность отказов λ=0,2∙10-4 1/час. Резерв пассивный с неизменной нагрузкой.
Определить потребную кратность резервирования k, чтобы вероятность безотказной работы была не ниже заданной Рзад=0,99 в течение работы изделия 10000 ч.
Решение:
Кратность резервирования может быть определена по формуле:
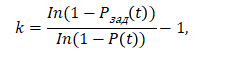
где P(t) вероятность безотказной работы элемента в течение времени t,
Pзад(t)=0,99 вероятность безотказной работы системы в течение времени t=10000 ч.
Для экспоненциального рас...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э