Случайная точка с координатами (X, Y) равномерно распределена в треугольнике с вершинами в точках с координатами (0;0), (-1 ;0) и (0;-2). Найти: а)совместную плотность двумерного распределения f(x,y);
- Теория вероятностей
Условие:
Случайная точка с координатами (X, Y) равномерно распределена в треугольнике с вершинами в точках с координатами (0;0), (-1 ;0) и (0;-2).
Найти:
а) совместную плотность двумерного распределения f(x,y);
б) одномерные (маргинальные) плотности f1 (x) и f2 (y) функции распределения F1(x) и F2 (y). нарисовать графики всех полученных функций;
в) ковариацию Cov(X,Y) и коэффициент корреляции ρxy. Установить, коррелированы/некоррелированы, зависимы или независимы случайные величины Х и Y
г) условную плотность f2 (y|x).
д) условные математическое ожидание M(Y|X) и дисперсию D(Y|X) случайной величины Y. Найти их значения при X = -0,8.
е) вероятность P(X<-0,3; Y>-0,7); P(X>Y).
Решение:
Область D треугольник с вершинами в точках (0;0),(-1;0),(0;-2):
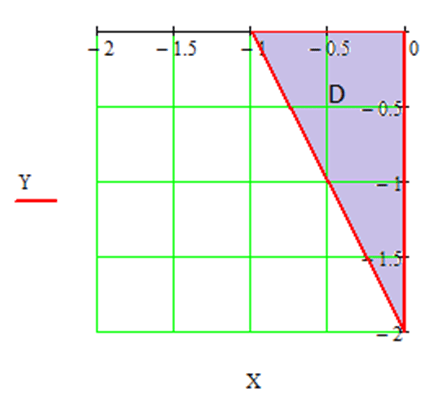
y = -2x - 2 соединяет точки (-1;0) и(0;-2).
а) Поскольку (X, Y) равномерно распределена в треугольнике, то плотность f(x,y) равна константе, т.е. единице, делённой на площадь области D, SD = 1.
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства