Условие:
Случайная величина Х задана интегральной функцией распределения F (x).
Найти:
1) вероятность того, что в результате испытания Х примет значения, принадлежащие заданному интервалу (a;b);
2) дифференциальную функцию распределения f (x);
3) математическое ожидание М(Х);
4) дисперсию D(X).
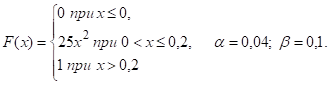
Решение:
1) Вероятность того, что случайная величина Х примет значение из интервала [a,b] равна:
P(a x b) = F(b) - F(a)
P(0.04 x 0.1) = F(0.1) - F(0.04) = 25∙0.12 - 25∙0.042 = 0.25 - 0.04 = 0.21
2) Найдем дифференциальную функцию распределения f(x), как производную от функции распределения...
