Условие:
Случайные величины Х и Y распределены по нормальному закону. По двум независимым выборкам из совокупностей Х и Y, объемы которых m=16 и n=20 соответственно, найдены выборочные средние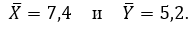 
Дисперсии известны: D(Х)= 4 и D(Y)=15. При уровне значимости α=0,01 проверить нулевую гипотезу М(Х)=М(Y) при конкурирующей гипотезе H1: М(Х)>М(Y).
Решение:
Критерием проверки нулевой гипотезы принимаем случайную величину
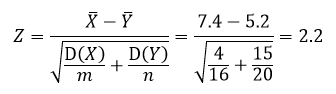
Данная случайная величина имеет нормальное распределение, поэтому находим критическую точку правосторонней критической области