Условие:
Случайные величины Х и Y имею следующий совместный закон распределения:
P(X=1, Y=1)=0,13; P(X=2, Y=1)=0,19
P(X=1, Y=2)=0,17; P(X=2, Y=2)=0,1
P(X=1, Y=3)=0,19; P(X=2, Y=3)=0,22
1) Выписать одномерные законы распределения случайных величин Х и Y, вычислить математическое ожидание E(X), E(Y) и дисперсии D(X), D(Y).
2) Найти ковариацию Cov(X,Y), и коэффициент корреляции ρ(X,Y).
3) Выяснить, зависимы или нет события {X=1}, {Y=X}
4) Составить условный закон распределения случайной величины Z=(Y|X=1), и найти E(Z), D(Z).
Решение:
1) Найдем одномерные законы распределения:
Сложив вероятности по строкам получим вероятности возможных значений Х: p(1)=0,13+0,17+0,19=0,49; р(2)=0,19+0,1+0,22=0,51.
Сложив вероятности по столбцам получим вероятности возможных значений Y: p(1)=0,13+0,19=0,32; р(2)=0,17+0,1=0,27; р(3)=0,19+0,22=0,41.
Получаем законы распределения составляющих
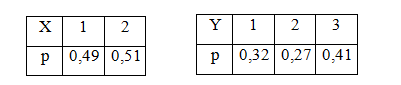
Контроль:
