Условие задачи
Случайная величина X имеет нормальное распределение с параметрами 
Требуется:
1) Составить функцию плотности распределения и построить ее график.
2) Найти вероятность того, что случайная величина в результате испытания примет значение, принадлежащее интервалу 
.
3)Найти вероятность того, что абсолютная величина отклонения значений случайной величины от ее математического ожидания не превысит 
.
Ответ
Плотность нормального распределения есть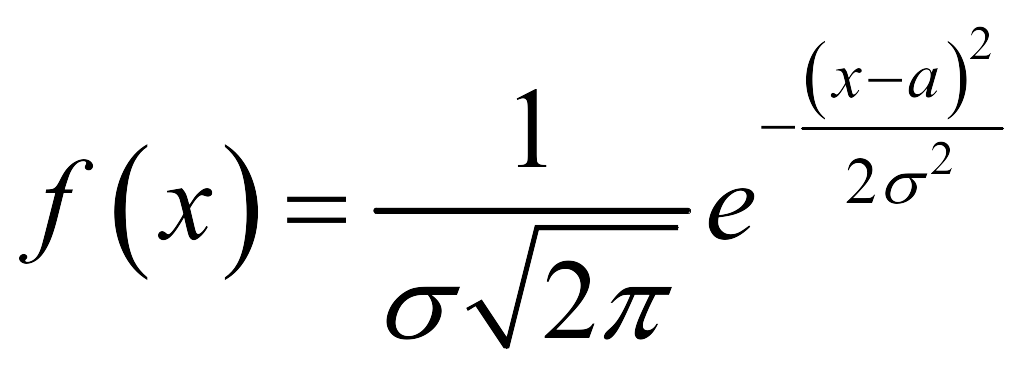 
, где 
- математическое ожидание, - среднее квадратическое отклонение, тогда получаем, что плотность нормально распределения есть
Потяни
