Условие задачи
В университете проведен анализ успеваемости студентов по математике. Для этого случайным образом выбрано 30 студентов, отдельно 15 девушек (Д) и 15 юношей (Ю) и результаты их аттестации по системе даны в следующих двух выборках. Объединив обе выборки в одну:
1. Составить интервальный вариационный ряд.
2. Построить гистограмму, эмпирическую функцию распределения и её график.
3. Найти средний бал, выборочную дисперсию и среднее квадратическое отклонение для объединенной выборки и отдельно для юношей и девушек.
Ю: 2,1 1,5 2,8 4,6 4,2 3,7 2,5 0,1 1,4 0 2,8 4,3 3,8 2,5 4,3
Д: 4,8 2,5 3,1 0,5 2,1 3,1 2,4 4,2 1,5 0,8 2,1 1,6 2,4 5,0 4,1
Ответ
1. Объем выборки n=30
Число интервалов вычислим по формуле Стерджеса
k=1+3,322lg(n)= 1+3,322lg(30)=5.9
Округляем до целого k=6.
Находим минимальный и максимальный элементы выборки
min 0
max 5
Вычисляем ширину интервала h=(max-min)/k=(5-0)/6=0,833
Рассчитываем интервалы и частоты попадания в каждый интервал. Это и будет интервальный ряд распределения
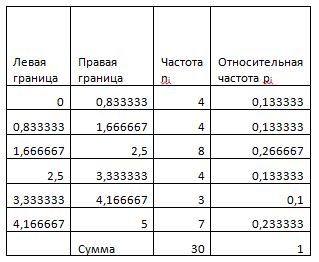
2. Для эмпирической функции распределения вычисляем н...
