Условие задачи
Страховая компания проводит страхование N однотипных объектов. Вероятность наступления страхового случая для каждого из объектов (независимо от других) за время t равна p. Найти вероятность того, что за время t:
1) страховой случай наступит от m1 до m2 раз;
2) относительная частота наступления страхового случая будет отклоняться от вероятности этого события по абсолютной величине менее чем на 0,05.
N=50, m1=10, p=0,3
Ответ
1) Для нахождения вероятности наступления страхового случая от 10 до 20 раз за время t, воспользуемся интегральной теоремой Лапласа.
Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p(0p1), событие наступит не менее m1 раз и не более m2 раз, приближенно равна:
,
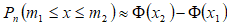Здесь - функция Лапласа, ,
