Условие:
Маша работает продавцом и кондитером в магазине леденцов. Маша умеет готовить леденцы в форме апельсинок, бананов и сердечек. Но вот беда! У Маши сегодня осталось всего лишь 6 кг сахара, из которого она делает сладости. Прибыль Маши вычисляется по следующей формуле: S = ab2c3, где a,b – массы в килограммах проданных леденцов апельсинок, бананов и сердечек соответственно. Учитывая то, что каждый день у Маши скупают все, что она приготовит, найдите максимальную прибыль, которую сможет получить Маша. (Считайте, что леденцы сделаны полностью из сахара).
Решение:
Имеем следующую задачу условной оптимизации:
S = ab2c3 max, a+b+c = 6
Составляем функцию Лагранжа:
L(a, b, c, ) = s(a, b, c) + (a, b, c)
В нашем случае (a, b, c) = a+b+c-6. Получили:
L(a, b, c, ) = ab2c3+(a+b+c-6)
Находим частные производные:
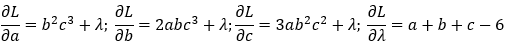
И приравниваем их к нулю:
