Условие задачи
1. В осветительную сеть параллельно включено 20 ламп. Вероятность того, что за время T лампа будет включена, равна 0,8. Пользуясь неравенством Чебышева, оценить вероятность того, что абсолютная величина разности между числом включенных ламп и средним числом (математическим ожиданием) включенных ламп за время T окажется: а) меньше трех; б) не меньше трех.
2. Вероятность того, что наудачу выбранная деталь окажется бракованной, при каждой проверке одна и та же и равна 0,2. Определить вероятность того, что среди 50 наугад выбранных деталей бракованных окажется не менее 6.
3. В осветительную сеть параллельно включено 20 ламп. Вероятность того, что за время T лампа будет включена, равна 0,8. Пользуясь неравенством Чебышева, оценить вероятность того, что абсолютная величина разности между числом включенных ламп и средним числом (математическим ожиданием) включенных ламп за время T окажется: а) меньше трех; б) не меньше трех.
4. Цех завода производит шарики для подшипников. За смену производится n=10000 шариков. Вероятность того, что один шарик окажется дефектным, равна 0,05. Причины дефектов для отдельных шариков независимы. Продукция проходит контроль сразу после изготовления, причем дефектные шарики бракуются и ссыпаются в бункер, а не бракованные отправляются в цех сборки. Определить, на какое количество шариков должен быть рассчитан бункер, чтобы с вероятностью 0,99 после смены он не оказался переполненным.
Ответ
1.Пусть случайная величина X число включенных ламп за время T.
Так как может быть два исхода: лампа или включена, или не включена, случайная величина X имеет биномиальное распределение. Найдём математическое ожидание и дисперсию данной случайной величины:
M(X)=20*0,8=16
D(X)=20*0,8*0,2=3,2
а) Используя неравенство Чебышева, получаем, что:
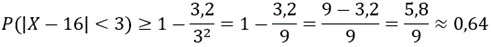
б) Данная вероятность является противоположной найденной в пунк...
