Условие задачи
В пирамиде находится n1 винтовок с оптическим прицелом и n2 – без оптического прицела. Из наугад выбранной винтовки спортсмен стреляет по цели. Вероятность поразить цель из винтовки с оптическим прицелом p1, из винтовки без оптического прицела p2.
1. Чему равна вероятность поразить цель?
2. Найти вероятность того, что цель поражена из винтовки с оптическим прицелом, если
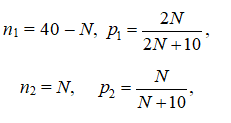
где N – 15.
Ответ
Обозначим события: А1- выбрана винтовока с оптическим прицелом, А2 выбрана без оптического прицела, В цель поражена
По условию (Воспользуемся классическим определением вероятности Всего винтовок 15, с оптическим прицелом 40-15=25):
Р(А1)= 25/40=0,625; Р(А2)= 15/40=0,375.
Эти события образуют полную группу событий, следовательно можно использовать формулу полной вероятности и формулу Байеса.
Условные вероятности (Вероятность поразить цель из винтовки с оптическим прицелом p)
