Вероятность наступления события в каждом из независимых испытаний равна ноль, восемь. Сколько нужно провести испытаний, чтобы с вероятностью ноль, девяносто пять можно было ожидать отклонение относительной частоты
«Вероятность наступления события в каждом из независимых испытаний равна ноль, восемь. Сколько нужно провести испытаний, чтобы с вероятностью ноль, девяносто пять можно было ожидать отклонение относительной частоты»
- Теория вероятностей
Условие:
Вероятность наступления события в каждом из независимых испытаний равна 0,8. Сколько нужно провести испытаний, чтобы с вероятностью 0,95 можно было ожидать отклонение относительной частоты появления события от его вероятности не больше, чем на 0,04.
Решение:
Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна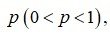 
абсолютная величина отклонения относительной частоты появления события от вероятности появления события не превысит положительного числа приближенно равна удвоенной функции Лапласа при
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э