Во многих системах эффективного кодирования изображений передаваемая информация содержит отличия значения сигнала в текущем пикселе от некоторых соседних. Для описания таких отличий используется распределение
«Во многих системах эффективного кодирования изображений передаваемая информация содержит отличия значения сигнала в текущем пикселе от некоторых соседних. Для описания таких отличий используется распределение»
- Теория вероятностей
Условие:
Во многих системах эффективного кодирования изображений передаваемая информация содержит отличия значения сигнала в текущем пикселе от некоторых соседних. Для описания таких отличий используется распределение Лапласа, которое в общем виде задается плотностью распределения:
pξ (x)=ce-λ|x-β| , λ>0
Найдите значение с, функцию распределения, числовые характеристики:
Mξ, Dξ, σξ, x1/2, вероятность P(a<ξ<b) попадания значения случайной величины в интервал (а,b), постройте
графики плотности и функции распределения.
β=2,5, λ=2, a=1, b=4
Решение:
подставляем заданные параметры:
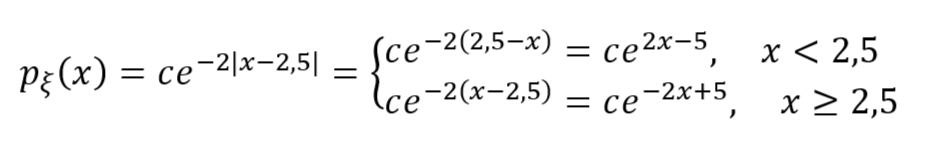
Определим значение величины с из свойства плотности функции распределения, называемого условием нормировки: 
Для заданной случайной величины:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э