Вычислить вектор мат. ожиданий и ковариационные характеристики данного случайного вектора. Найти аффинное преобразование, переводящее исходный случайный вектор в стандартный нормальный.
- Теория вероятностей
Условие:
Плотность двумерного нормального распределения имеет вид:
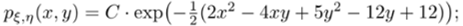
1. Вычислить вектор мат. ожиданий и ковариационные характеристики данного случайного вектора.
2. Найти аффинное преобразование, переводящее исходный случайный вектор в стандартный нормальный.
3. Найти ортогональное преобразование, переводящее соответствующий центрированный случайный вектор в вектор с независимыми компонентами.
4. Вычислить характеристики совместного распределения случайного вектора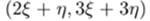 
и записать его плотность.
5. Найти условное распределение ξ при условии η.
6. Даны квадратичные формы
а. Вычислить распределения (х.ф-ии.) распределений Q1 и Q2, классифицировать их.
б. Определить, являются ли Q1 и Q2 независимыми.
Решение:
1. Вычисление вектора мат. ожиданий и ковариационных характеристик С.В.
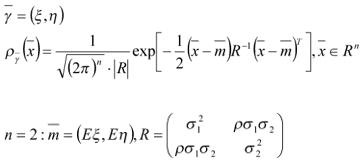
Находим неизвестные величины.
Выделим полные квадраты в показателе степени:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства