Газовая трехкомпонентная смесь, имеющая состав m1, m2, m3 (в кг), совершает в тепловом двигателе круговой процесс (цикл) по преобразованию теплоты в механическую работу. Ряд значений параметров состояния смеси в отдельных точках цикла приведены ниже.
- Теплоэнергетика и теплотехника
Условие:
Газовая трехкомпонентная смесь, совершает в тепловом двигателе круговой процесс (цикл) по преобразованию теплоты в механическую работу. Ряд значений параметров состояния смеси в отдельных точках цикла приведены ниже.
Исходные данные:
N2=5 кг
CO =1 кг
CO2 = 3 кг
P1= 3 бар
P5 =3 бар
T5 = 1050 К
P2 = 5,6 бар
T2 = 340 К
P3 = 12,2 бар
v4 =4/3 v3, м3/кг

В цикле предполагается, что:
1) процессы (2→3) и (5→1) – изохорные, (3→4) изобарный, (1→2) и (4→5) – политропные;
2) если по условиям варианта P2 = P3 или P5 = P1,то в цикле отсутствуют, соответственно, процессы (2→3) и (5→1);
3) при T = const политропный процесс превращается в изотермический (n = 1);
4) если по результатам расчетов n = k (показатель политропы равен показателю адиабаты), то политропный процесс рассчитывается как адиабатный (dq = 0).
Требуется:
1) Определить удельную газовую постоянную смеси и её «кажущуюся» молекулярную массу.
2) Определить коэффициент полезного действия цикла.
3) Определить коэффициент полезного действия цикла Карно в интервале температур цикла (от Tmax до Tmin).
4) Построить цикл в P-v и T-s диаграммах (с расчетом 2х - 3х промежуточных точек в каждом процессе).
Решение:
Так как P5 = P1 , то цикл имеет следующие процессы:
1-2 политропный
2-3 изохорный
3-4 изобарный
4-1 политропный
Массовые доли
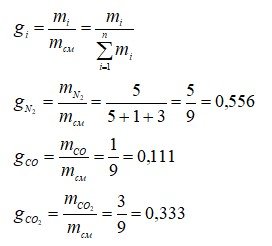
Молекулярная масса
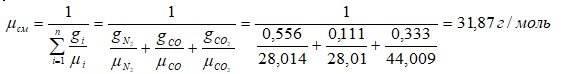
Универсальная газовая постоянная
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства